AHP فازی
AHP فازی چیست
فرایندهای ذهنی معمول برای حل مسائلی که در زندگی روزمره ما را یاری می کنند، ممکن است در موضوعات پیچیده که نظرات و ایده های بسیار متفاوت وجود دارد ما را گمراه کنند. آنچه ما بدان نیازمندیم شیوه پیچیده برای فکر کردن نیست. زیرا حتی تفکر ساده خود بسیار مشکل ساز است و باید چارچوبی وجود داشته باشد که ما را قادر سازد تا در خصوص مسائل پیچیده به شیوه ای ساده بیاندیشیم.فرایند تحلیل سلسله مراتبی یا (Analytical Hierarchy Process) چنین چارچوبی را ایجاد میکند. این فرایند به ما کمک میکند تا بتوانیم تصمیمات مناسب برای موضوعات پیچیده را با ساده نمودن و هدایت مراحل تصمیم گیری اتخاذ کنیم.AHP روشی است که در آن یک وضعیت پیچیده، به بخشهای کوچکتر آن تجزیه شده ، سپس این اجزا در یک ساختار سلسله مراتبی قرار می گیرد. در این روش به قضاوتهای ذهنی با توجه به اهمیت هر متغیر مقادیر عددی اختصاص داده، متغیرهایی که بیشترین اهمیت را دارند، مشخص می شوند. به عبارت دیگر ترتیب اولویت متغیرها تعیین می شود. به این ترتیب، به کمک AHP می توان مسائل پیچیده ای که دربرگیرنده عوامل متعددند را درک نمود. به طور کلی انسانها دو رویکرد اساسی را در تجزیه و تحلیل به کار می برند که شامل رویکرد قیاسی (DeductiveApproach) و رویکرد سیستمی (Inductive Approach) است. به کارگیری هر دو رویکرد سیستمی و قیاسی در درک یک سیستم پیچیده بسیار موثر خواهد بود و ترکیب این دو رویکرد از طریق فن AHP امکان پذیر است.
عدم اطمینان موجود در قضاوتهای ترجیحی، عدم اطمینان اولویت بندی آلترناتیوها را افزایش می دهد و به همان نسبت، تعیین توافق (ثبات منطقی) اولویتها را مشکل می سازد. مطالعات زیادی از جنبه های مختلف انجام شد و در نهایت منجر AHP فازی شد. AHP فازی برای برای اجتناب از این مخاطرات عملکردی توسعه یافت تا مسایل سلسله مراتبی دارای ابهام را حل کند.
در این روش بر اساس جواب هایی که تصمیم گیرندگان به سئوالات می دهند، مقادیر مثلثی فازی، جایگزین داده های مبهم می شوند و برای یک سطح خاص سلسله مراتب، ماتریس مقایسات زوجی تشکیل می شود. در رویکرد منطق فازی، برای هر مقایسه زوجی، نقطه تقاطع پیدا می شود و سپس مقدار عضویت نقطه با وزن آن برابر می شود.
بعد از تعریف معیارها، یک پرسشنامه تهیه می شود تا سطوح اهمیت این معیارها تعیین شود. برای ارزیابی سئوالات، افراد تنها متغیر توصیفی مربوطه را انتخاب میکنند، سپس گزینه های منتخب، با توجه به طیف های فازی که شامل اعداد فازی مثلثی است، تبدیل می شوند و برای انجام محاسبات و تحلیل نتایج، تعمیم داده می شوند.

انواع اعداد در AHP فازی
در روش ahp فازی در اکثر مقالات از دو نوع عدد فازی استفاده کرده اند :1- عدد فازی مثلثی، 2-عدد فازی ذوزنقه ای.
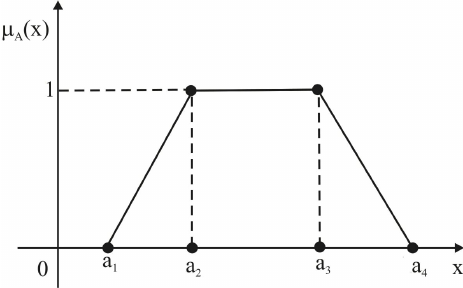
عدد فازی ذوزنقه ای به صورت یک عدد با 4 درایه مطرح می شود که تابع عضویت آن 4 تابعی است. در واقع در این تابع عضویت مقادیر بین m1 و m2 دارای درجه عضویت 1 هستند فرض کنید فردی را ما جوان در نظر بگیریم که بین 20 تا 30 باشد حالا دو حد وسط را اگر 22 تا 28 در نظر بگیریم در این بازه صددرصد جوان هست.
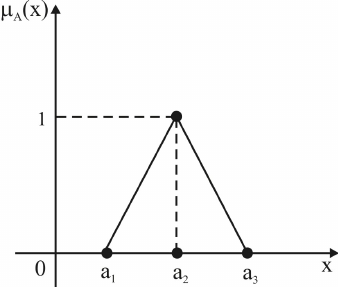
ساده ترین و در عین حال پرکاربردترین عدد فازی، مثلثی می باشد این عدد فازی دارای 3 درایه می باشد که تابع عضویت آن 3 تابعی است. این مدل عدد فازی تقریبا در همه مقالات و پایان نامه ها مورد استفاده قرار می گیرد. در این مدل عدد m دارای مقدار تابع عضویت 1 است.
آموزش AHP فازی
مراحل روش تحلیل سلسله مراتبی فازی چانگ به شرح زیر است:
گام 1: رسم نمودار سلسله مراتبی
گام 2: تعریف اعداد فازی به منظور انجام مقایسات زوجی
گام 3: تشکیل ماتریس مقایسات زوجی با به کارگیری اعداد فازی
اگر چند خبره وجود داشته داشته باشد، درایه های ماتریس مقایسه زوجی جامع که در روش تحلیل سلسله مراتبی فازی به کار می رود، یک عدد فازی مثلثی است که مولفه اول(l) آن حداقل نظرات، مولفه دوم (m) میانگین اعداد و عدد سوم (u) حداکثر اعداد می باشد.
گام 4: محاسبه برای هر یک از سطرهای ماتریس مقایسه زوجی
مرحله 5: محاسبه درجه بزرگی ها نسبت به همدیگر
گام 6: محاسبه وزن معیارها و گزینه ها در ماتریس مقایسه زوجی
گام 7: محاسبه بردار وزن نهایی
برای محاسبه بردار وزن نهایی باید بردار وزن محاسبه شده در مرحله قبل را نرمالیزه کرد.
نرخ ناسازگاری در AHP فازی
در روش AHP فازی چانگ عموما از نرخ ناسازگاری گوگوس و بوچر استفاده می شود.
نرخ ناسازگاری گوگوس و بوچر : گوگوس و بوچر در سال 1998 پیشنهاد دادند برای بررسی سازگاری، دو ماتریس (عدد میانی و حدود عدد فازی) از هر ماتریس فازی مشتق و سپس سازگاری هر ماتریس بر اساس روش ساعتی محاسبه شود.
مراحل محاسبه نرخ سازگاری گوگوس و بوچر ماتریسهای فازی مقایسات زوجی به قرار زیر است:
مرحله ۱: در مرحله اول ماتریس مثلثی فازی را به دو ماتریس تقسیم کنید. ماتریس اول از اعداد میانی قضاوتهای مثلثی تشکیل میشود و ماتریس دوم شامل میانگین هندسی حدود بالا و پایین اعداد مثلثی میشود.
مرحله ۲: بردار وزن هر ماتریس را با استفاده از روش ساعتی به ترتیب زیر محاسبه کنید.
برای محاسبه نرخ ناسازگاری (CR)، شاخص CI را بر مقدار شاخص تصادفی (RI) تقسیم کنید. در صورتی که مقدار حاصل کمتر از 0/1 باشد، ماتریس سازگار و قابل استفاده تشخیص داده میشود.
ساعتی برای بهدست آوردن مقادیر شاخصهای تصادفی (RI)، ۱۰۰ ماتریس را با اعداد تصادفی و با شرط متقابل بودن ماتریسها تشکیل داده و مقادیر ناسازگاری و میانگین آنها را محاسبه نمود. اما از آنجا که مقادیر عددی مقایسات فازی همواره عدد صحیح نیستند و حتی در این صورت هم میانگین هندسی، آنها را عموماً به اعداد غیرصحیح تبدیل میکند،
حتی در صورت استفاده از مقیاس (۹-۱) ساعتی نیز نمیتوان از جدول شاخصهای تصادفی(RI) ساعتی استفاده کرد. بنابراین گوگوس و بوچر با تولید ۴۰۰ ماتریس تصادفی مجدداً جدول شاخصهای تصادفی(RI) را برای ماتریسهای مقایسات زوجی فازی تولید کردند.

AHP فازی در اکسل
برای انجام AHP فازی در اکسل اگر چند خبره وجود داشته باشد ابتداد باید مقایسات زوجی تمامی خبرگان را وارد نرم افزار کرد و سپس از آن ها میانگین گرفت و میانگین را وارد محاسبات AHP فازی کرد. با توجه با روش AHP فازی چانگ ابتدا Si هر سطر و Si کلی را محاسبه کرد. در مرحله بعد درجه بزرگی Si ها نسبت به هم محاسبه شده و در نهایت وزن فازی و وزن نهایی به دست می آید و از طریق وزن نهایی می توان رتبه بندی را انجام داد.
با توجه به پیچیدگی های محاسبات AHP فازی اگر با کد نویسی در اکسل آشنایی ندارید پیشنهاد نمی شود از excel استفاده کنید زیرا با تغییر در تعداد معیار یا زیر معیار یا گزینه ها محاسبات شما به هم می خورد.

AHP فازی در متلب
برای اجرای AHP فازی در متلب ابتدا می بایست نرم افزار matlab با حجم تقریبا 5 گیگابایت را دانلود کنید. با توجه به اینکه در برنامه متلب toolbox یا جعبه ابزار ahp فازی وجود ندارد باید بر اساس پروژه خود در محیط برنامه نویسی متلب کد نویسی انجام داده و پروژه خود را پیاده سازی کنید.

AHP فازی pdf
در زیر چند نمونه کاربردهای ahp فازی که در قالب مقاله pdf در زیر آورده شده است:
انتخاب چند معیاره تامین کنندگان با استفاده از AHP فازی
کاربرد روش های فازی و AHP برای جانمایی مدارس ابتدایی در ناحیه یک آموزشی شهر کرمان
کاربرد روش تحلیل سلسله مراتبی فازی در تعیین گزینه بهینه نمک زدایی از آب های لب شور
کاربرد فرایند تحلیل سلسله مراتبی فازی در اولویت بندی عوامل مؤثر بر انتخاب سهام در بورس اوراق بهادار تهران از دیدگاه سهامداران
بالانس خط دمونتاژ مبتنی بر مدل کانو و روش های تصمیم گیری چند معیاره فازی (مورد مطالعه: خط بازیافت ضایعات الکترونیکی)
انتخاب مصالح جداره بیرونی ساختمان مسکونی در اقلیم گرم و خشک ایران با استفاده از روش تحلیل سلسله مراتبی فازی (FAHP)
ارزیابی مسیرهای حمل و نقل جادهای مواد خطرناک با رویکرد ریسک در محیط فازی (مطالعه موردی : استان زنجان)
شناسایی و اولویتبندی چالشهای تحقق سیاستگذاری داده حکومتی باز در ایران: کاربست روش تحلیل سلسلهمراتبی و تاپسیس فازی
مقایسه جایگاه ایران با کشورهای منطقه غرب آسیا از جهت مشارکت در حکمرانی اقتصادی بین المللی
تحلیل و ارزیابی کاربرد روش تحلیل سلسله مراتبی فازی در اولویت بندی سناریوهای توسعه گردشگری روستایی
حسابداری مدیریت زیست محیطی با رویکرد یکپارچه برای طراحی تولید سبز با استفاده از تحلیل سلسله مراتبی فازی
تعیین معیارهای ارزیابی عملکرد کارکنان یک شرکت تولیدی
تحلیل ارزش مشتری در بانک با استفاده از تکنیک داده کاوی و تحلیل سلسله مراتبی فازی
شناسایی و اولویت بندی بافت فرسوده شهری با استفاده از مدل تحلیل سلسله مراتبی فازی(FAHP)
ارزیابی مؤلفه های کیفیت فضای شهری بر میزان مطلوبیت مسیرهای پیاده گردشگری (مورد پژوهی اولویت بندی مسیرهای گردشگری پیاده در شهر اصفهان)
تحلیل رقابت جویی و انتخاب استراتژی رقابتی مبتنی بر مدل نیروهای رقابتی پورتر، تحلیل سلسله مراتبی فازی و تحلیل پوششی داده
ارزیابی موانع توسعۀ بازاریابی ورزشی در ایران
تحلیل ارزش مشتری در بانک با استفاده از تکنیک داده کاوی و تحلیل سلسله مراتبی فازی
بررسی وضعیت فضای کسب و کار در استان آذربایجان شرقی و راهکارهای ارتقای آن
تحلیل فضایی- مکانی مدل های تصمیم گیری چند معیاره فازی در مکانگزینی کتابخانه عمومی مطالعه موردی: منطقه چهار کلانشهر تبریز
همانگونه که از نمونه مقالات بالا مشخص است AHP فازی کاربرد گسترده ای در زمینه های گوناگون دارد از جمله در شهرسازی، حسابداری، شهرسازی، صنایع،علوم انسانی، گردشگری، بازاریابی، سیاست، آموزش، محیط زیست و …